Von den Quadraten (Häuschen) zu den Rechtecken

Das betrachtete Intervall (Zeitraum) wird in N gleiche Teile unterteilt. Die Zahl N kann frei gewählt werden. In der Abbildung rechts wird zum Beispiel das Intervall [2..8] in 6 Teile geteilt. Wir betrachten nun diese Teilintervalle als Rechtecke. Die Summe der Flächen dieser Rechtecke entspricht näher- ungsweise der Fläche unter der Kurve.

• N Rechtecke

  

• Algorithmus D1

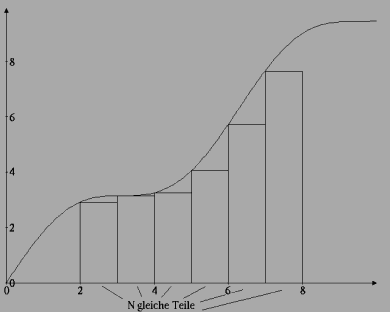
  Eingabe: f : Funktion
           a : linker Rand
           b : rechter Rand
           n : Anzahl Teilintervalle
  
  area := 0;
  x := a;
  s := (b-a)/n;            (* Breite eines Intervalles *)
  WHILE (n>0) DO
      area := area + f(x)*s;
      x := x+s;            (* nächstes Intervall       *)
      n := n-1;
  END
  
  Ausgabe: area = Näherung der Fläche
  

Wieviele Intervalle soll man wählen? Offensichtlich gilt: Je mehr Intervalle, umso genauer wird die Fläche berechnet und umso grösser wird der Rechenaufwand! Man muss sich also entscheiden: Grössere Genauigkeit oder schnellere Berechnung...